旋振筛是一个多维多自由度振动系统，工作方式较之其他类型的筛分机有本质的不同。有关它的动力学和筛分机理研究问题一直未能得到解决…。由于筛体上各点的振动情况不尽相同，故无法用经典的求解常微分方程的方法来研究物料在筛面上的运动轨迹，必须要解一组非线性微分方程。本文将发展一数值递推法，借助计算机来对一般情况下物料在旋振筛面上的运动轨迹进行理论分析研究。
　　旋振筛筛体的运动分析：
　　1、筛体的运动微分方程
　　在一定条件下 ， 旋振筛可以简化为一个六 自由度的无阻尼线性强迫振动模型。如果再适当地选择坐标系( 图 I ) ， 则可以获得如下解耦的运动微分方程组，式中：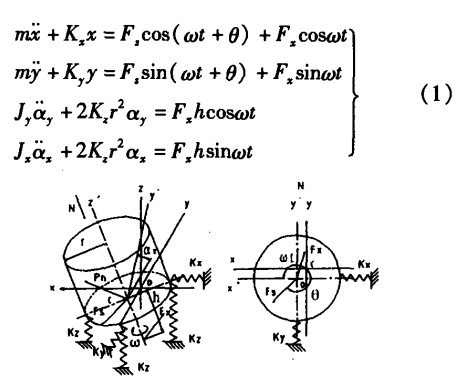

　　　　　　　　　　图１　旋振筛动力学模型
　　x,Y分别为振动体( 包括筛体和振动电机等) 的质心在水平面内二个相互垂直方向的位移；a_x,a_y分别为振动体绕轴和Y轴的转角；j_x，j_y分别为振动体绕x轴和y轴的转动惯量； m为振动体的质量。

　　物料在筛面上的运动轨迹：
　　分析时基于下面三个假设：
　　( 1 ) 筛面只具有和筛体相同的振动；
　　( 2 ) 物料为单颗体；
　　( 3 ) 物料起跳时， 只具有物料起跳瞬时在筛面 上所处点的速度， 即相对滑动影响暂不考虑。 3
　　1、物料起抛速度
　　设P点即为物料的起抛点， 则物料的起抛速度为：

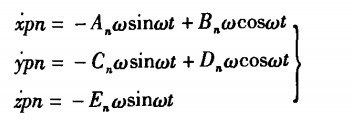
　　2、物料的始抛角
　　起抛时， 物料的受力情况应满足下面的不等式：
　　
　　物料起抛的最大高度H_mas和达到此高度的时间t₂
　　……

　　影响物料的运动轨迹的因素是很多的， 但实际使用时， 便于调整的还是工作夹角0°利用计算机对轨迹方程进行数值迭代求解，当轨迹影响系数P_x和P_y结果为：均小于1时， 而且φ=90 ( 这时物料更易起抛) ， 则 Δ( x_n) 就呈余弦特性， Δ( y_n ) 就呈正弦特性。随着工作夹角θ从 O°变化到 360°， 差不多每过45°就可以获得一种新的轨迹，这样我们一共可以获得物料在筛面上的八种运动轨迹， 和实验结果是完全吻合。
　　当θ为45°时， 物料的运动轨迹为螺旋向外， 这时的筛分效率更高， 所以旋振筛都是选用这个工作夹角。